Life has its own fate, and meeting may not be accidental.

0%

pta-7-52 求解迷宫从入口到出口的所有最短路径(DFS)

发表于 更新于 分类于   |   字数统计: 933(字)   |   阅读时长: 4(分) Valine：

求解迷宫从入口到出口的一条最短路径。输入一个迷宫，求从入口通向出口的一条可行最短路径。为简化问题，迷宫用二维数组 int maze[10][10]来存储障碍物的分布，假设迷宫的横向和纵向尺寸的大小是一样的，并由程序运行读入, 若读入迷宫大小的值是n（3<n<=10），则该迷宫横向或纵向尺寸都是n，规定迷宫最外面的一圈是障碍物，迷宫的入口是maze[1][1]，出口是maze[n-2][n-2], 若maze[i][j] = 1代表该位置是障碍物，若maze[i][j] = 0代表该位置是可以行走的空位（0<=i<=n-1, 0<=j<=n-1）。求从入口maze[1][1]到出口maze[n-2][n-2]可以走通的所有最短路径条数。要求迷宫中只允许在水平或上下四个方向的空位上行走，走过的位置不能重复走。 如下这样一个迷宫：

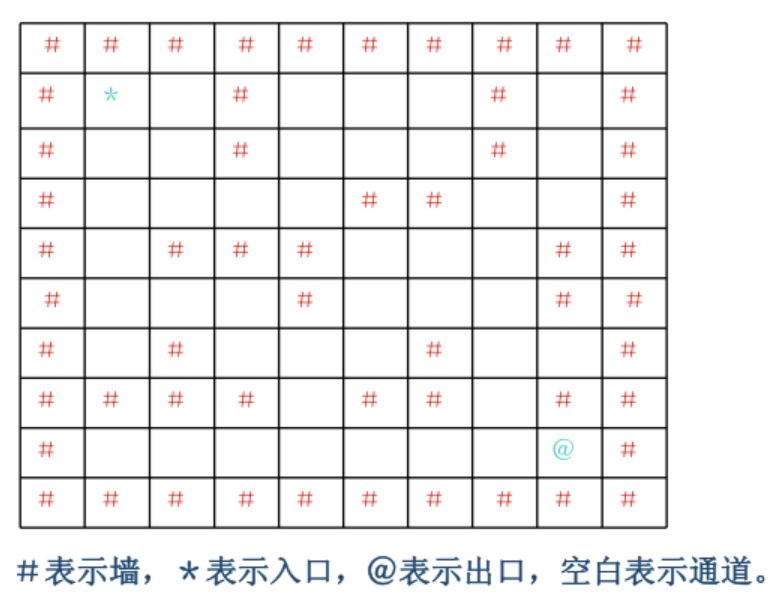
对应的二维数组表示： 

1
2
3
4
5
6
7
8
9
10
11
12
  int maze[10][10]={
{1,1,1,1,1,1,1,1,1,1},
{1,0,0,1,0,0,0,1,0,1},
{1,0,0,1,0,0,0,1,0,1},
{1,0,0,0,0,1,1,0,0,1},
{1,0,1,1,1,0,0,0,1,1},
{1,0,0,0,1,0,0,0,1,1},
{1,0,1,0,0,0,1,0,0,1},
{1,1,1,1,0,1,1,0,1,1},
{1,0,0,0,0,0,0,0,0,1},
{1,1,1,1,1,1,1,1,1,1}
  };

输入格式：

输入迷宫大小的整数n, 以及n行和n列的二维数组（数组元素1代表障碍物，0代表空位）。

输出格式：

输出按规定可以走通的所有最短路径条数。若没有通路，输出：0。

输入样例：

1
2
3
4
5
4
1 1 1 1
1 0 1 1
1 0 0 1
1 1 1 1

输出样例：

1

输入样例：

1
2
3
4
5
6
7
8
9
10
11
10
1 1 1 1 1 1 1 1 1 1
1 0 0 1 0 0 0 1 0 1
1 0 0 1 0 0 0 1 0 1
1 0 0 0 0 1 1 0 0 1
1 0 1 1 1 0 0 0 0 1
1 0 0 0 1 0 0 0 0 1
1 0 1 0 0 0 1 0 0 1
1 0 1 1 1 0 1 1 0 1
1 1 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1 1

输出样例：

1

代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include<bits/stdc++.h>
using namespace std;
int n,flag=0,Min,sum;
int Map[30][30]; 
int vis[30][30];
int dir[4][2]={0,1,0,-1,-1,0,1,0};
void dfs(int x,int y,int step){     //求最短路径
	if(step>Min){
		return;
	}
	if(x==n-2&&y==n-2){
		Min=step;
		return;
	}
	for(int i=0;i<4;i++){
		int xx=x+dir[i][0];
		int yy=y+dir[i][1];
		if(xx<0||yy<0||xx>=n||yy>=n){
			continue;
		}
		if(!vis[xx][yy]&&Map[xx][yy]==0){
			vis[xx][yy]=1;
			dfs(xx,yy,step+1);
			vis[xx][yy]=0;
		}
	}
	return;
}
void dfs1(int x,int y,int step){        //求相同路径
	if(x==n-2&&y==n-2&&step==Min){
		sum++;
		return;
	}
	for(int i=0;i<4;i++){
		int xx=x+dir[i][0];
		int yy=y+dir[i][1];
		if(xx<0||yy<0||xx>=n||yy>=n){
			continue;
		}
		if(!vis[xx][yy]&&Map[xx][yy]==0){
			vis[xx][yy]=1;
			dfs1(xx,yy,step+1);
			vis[xx][yy]=0;
		}
	}
	return;
}
int main(){
	scanf("%d",&n);
	memset(vis,0,sizeof(vis));
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			scanf("%d",&Map[i][j]);
		}
	}
	vis[1][1]=1;
	Min=10000;
	dfs(1,1,0);
	if(Min==10000){         //不存在最短路
		printf("0\n");
	}
	else{
		memset(vis,0,sizeof(vis));
		sum=1;
		vis[1][1]=1;
		dfs1(1,1,0);        //求同最短路一样的路
		printf("%d",sum);
	}
	return 0;
}